Un esempio Prima di concludere, anche se non servirebbe per informatica, vediamo almeno un esempio classico di Algebra di Boole non binaria ed anche un esempio di insieme parzialmente ordinato Dato l'insieme A≡{a,b,c}, consideriamone l'insieme potenza ℘(A)≡{{∅}, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b.c} } Tale insieme, dotato delle normali operazioni di unione, intersezione e complementare e' un algebra di Boole con 0 che corrisponde all'insieme vuoto {∅} ed 1 che corrisponde all' insieme universo {a,b.c} Vediamolo nei particolari Voglio dimostrare che (℘(A); ∪, ∩ , ') e' un algebra di Boole ' e' l'operazione di passaggio al complementare e corrisponde alla differenza fra l'insieme universo e l'insieme considerato, cioe' ad esempio {a,b}'={c}={a,b,c}\{a,b} Chiamiamo x, y, z, .. dei generici elementi di ℘(A); e controlliamo che valgono le proprieta' Legge commutativa x ∪ y = y ∪ x a ∩ y = y ∩ x      Vero per la commutativita' delle operazioni unione ed intersezione fra insiemi Legge distributiva x ∪ (y ∩ z) = (x ∪ y) ∩(x ∪ z)     x ∩(y ∪ z) = (x ∩ y) ∪ (x ∩ z) sono le normali proprieta' distributive fra insiemi Leggi dell'identita' x ∪ {∅} = x     cioe' {∅} corrisponde allo 0 x ∩ {a,b.c} = {a,b.c}     cioe' {a,b.c} corrisponde ad 1 Leggi del complemento x ∪ x' = {a,b.c} x ∩ x' = {∅} Infatti la somma di due complementari da' l'universo e l'intersezione di due complementari da' l'insieme vuoto Essendo soddisfatte tutte le proprieta' la struttura (℘(A); ∪, ∩ , ') e' un algebra di Boole Consideriamo, infine, la normale relazione di inclusione in senso largo ⊆ (contenuto od uguale) fra insiemi Diremo che tale relazione e' di ordine parziale su ℘(A) e che {℘(A); ⊆} e' un insieme parzialmente ordinato infatti, chiamati x, y, z elementi qualunque di ℘(A) valgono le 3 proprieta': riflessiva x ⊆ x    ∀ x ∈ ℘(A) ogni insieme e' contenuto od uguale a se' stesso antisimmetrica se x⊆y e y⊆x ⇒ x=y    ∀ x,y ∈ ℘(A) transitiva x⊆y, y⊆z ⇒ x⊆z    ∀ x,y,z ∈ ℘(A) Se il primo iniseme e' contenuto od uguale ad un secondo ed il secondo insieme e' contenuto od uguale ad un terzo ne segue che il primo insieme e' contenuto od uguale al terzo 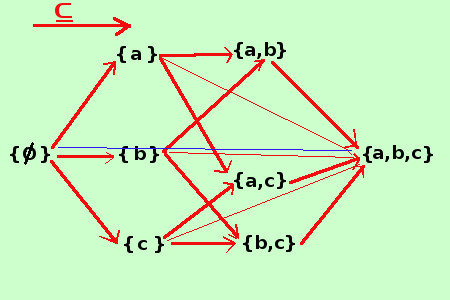Tale relazione ⊆, induce sull'insieme ℘(A) un ordine che va dagli insiemi piu' piccoli agli insiemi piu' grandi, e tale relazione e' solo parziale perche' esistono elementi non confrontabili: ad esempio {a} non e' confrontabile con {b,c} A destra una rappresentazione grafica dell'insieme in questione: le linee rosse con verso da sinistra a destra indicano la relazione di inclusione: per ragioni grafiche per l'insieme vuoto (che e' contenuto in tutti gli insiemi) non ho messo le linee di inclusione limitandomi ad una linea azzurra fino all'insieme universo notare la forma a cubo con i vertici corrispondenti agli elementi di ℘(A)