|
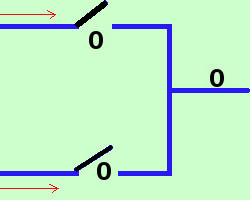
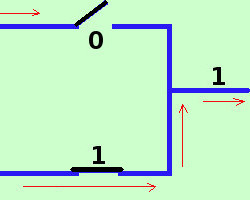
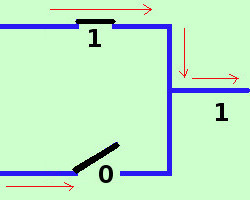
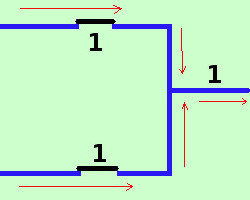
E' la somma definita nell'algebra di Boole a+b corrisponde alla disgiunzione inclusiva in logica Possiamo rappresentarlo con il circuito 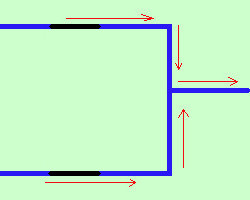
infatti abbiamo le 4 possibilita'
in forma normale disgiuntiva completa possiamo pensarla come a+b = a'b + ab' +ab per esercizio dimostriamolo algebricamente a+b = (a+b)(a+a') = moltiplico per (a+a')=1 per la prima legge del complemento = aa + aa' + ab +ab' = sviluppo; aa=a per la seconda legge dell'idempotenza e aa'=0 per la seconda legge del complemento = a + ab + a'b = so che a+ab=a per la prima legge di assorbimento = a + a'b = = a(b+b')+a'b = moltiplico per (b+b')=1 il primo termine ed ottengo = ab + ab' +a'b cioe' ordinando come avevamo gia' visto nella pagina della tabella a+b = a'b + ab' +ab |