|
Quella che abbiamo dato nella pagina precedente e' una definizione mediante intorni ed e' valida sempre per ogni tipo di limite; ma e' possibile dare, per una successione convergente, una definizione di limite piu' "algebrica"che puo' essere meglio utilizzata negli esercizi
Intuitivamente significa che una successione a1, a2, a3, ..... ak, ..... tende al limite finito a se preso un intorno piccolo di a (largo ε) da un certo termine ak in poi tutti i termini della successione cadono dentro tale intorno 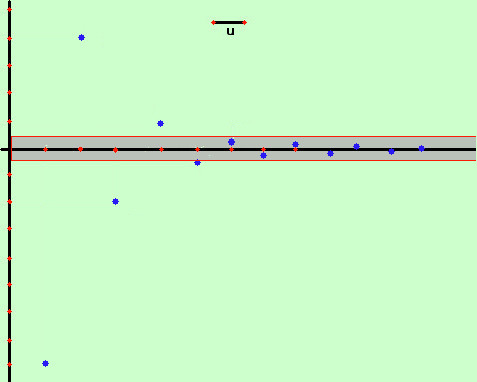 Esempio: considero la successione
Esempio: considero la successione-8, +4, -2, +1, -½, +¼.... (-½)n-4, ..... Se vuoi vedere perche' il termine generico e' (-½)n-4 Se guardi la figura a destra vedi che gia' prendendo come valore di ε sulle ordinate circa ±1/2 gia' il termine 1/4 della successione cade dentro la striscia colorata come tutti i termini successivi, che si avvicinano tanto a 0 che non posso nemmeno disegnarli La successione tende a 0 perche' se considero un numero piccolo, tipo 1/1000 (un millesimo) esiste un termine della successione oltre il quale tutti i termini cadono a meno di un millesimo da 0 tale termine sara' 1/512; il termine successivo 1/1024 e' piu' vicino a zero di un millesimo come tutti i termini seguenti Ti scrivo i primi 15 termini della successione, cosi' puoi verificare da solo
Il tal caso diremo che il limite e' finito e scriviamo limk→∞ ak = a nel nostro caso la successione considerata ha valore 0 Poiche' possiamo indicarla come -8·(-½)k-1 potremo scrivere limk→∞ -8·(-½)k-4 = 0 Da notare che per indicare il termine generico dello sviluppo della successione uso la lettera n, mentre per fare il limite del termine generico uso la lettera k: e' una pignoleria, pero' cosi' indico in modo diverso due cose diverse |

|

|

|

|