Limite infinito di una successione Diremo che una successione a1,a2,a3,..... ak, ..... tende al limite infinito ∞ se preso un intorno di ∞ da un certo termine ak in poi tutti i termini della successione cadono dentro tale intorno Anche qui e' possibile dare una definizione di limite piu' "algebrica"che puo' essere meglio utilizzata negli esercizi 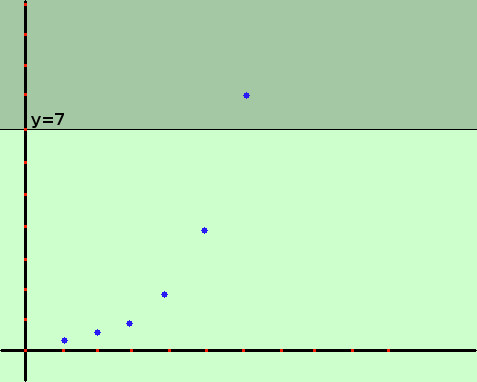Definizione diremo che la successione a1, a2,........ an,....... tende al limite infinito ∞ se considerato un numero M positivo grande a piacere, esiste in sua corrispondenza un numero kM∈N tale che quando |an|> M abbiamo n >kM In simboli: limn→∞ an = ∞     ⇔     |an|> M   ⇒   n > kM Esempio: considero la successione ¼, ½, 1, 2, 4, 8, 16, 32, 64,..... 2n-3, ..... Se vuoi vedere perche' il termine generico e' 2n-3 Se guardi la figura a destra vedi che gia' prendendo come valore dell'intervallo sulle ordinate y>7 gia' il termine 8 della successione cade dentro la striscia colorata come tutti i termini successivi, che si avvicineranno sempre piu' a +∞ La successione tende a +∞ perche' se considero un numero grande, tipo 1000 esiste un termine della successione oltre il quale tutti i termini cadono oltre la striscia y>1000 tale termine sara' 512; il termine successivo 1024 e' oltre 1000 come tutti i termini seguenti Ti scrivo i primi 15 termini della successione, cosi' puoi verificare da solo ¼, ½, 1, 2, 4, 8, 16, 32, 64, 128, 256, 1024, 2048, 4096, 8192, ....... Il tal caso diremo che la nostra successione ha limite infinito e scriviamo limk→∞ ak = ∞ nel nostro caso la successione considerata converge al valore +∞ Poiche' possiamo indicarla come 2k-3 potremo scrivere limk→∞ 2k-3 = +∞