tipi di successioni a limite finito Per capirci meglio nei grafici delle successioni introduciamo il concetto di asintoto orizzontale come retta orizzontale cui si avvicinano sempre piu' i termini della successione senza mai toccarla; Per ogni esempio abbiamo varie possibilita': il limite a puo' essere positivo, negativo o nullo: l'asintoto orizzontale y = a sara' sopra, sotto oppure coincidera' con l'asse delle x: per avere ogni possibilita' bastera' alzare od abbassare la figura rispetto all'orizzontale Distinguiamo i casi Successione decrescente con limite finito Esempio: consideriamo 2 ,   3 2 ,   4 3 ,   5 4 , ........ n+1 n ,  ..... Essa ha come limite il valore 1: i suoi termini si avvicinano al valore 1 decrescendo Da un certo momento in poi tutti i termini della successione sono contenuti nella striscia colorata (intorno superiore di 1 che posso restringere quanto voglio), quindi posso scrivere limk→∞ k+1 k = 1 Successione crescente con limite finito Esempio: consideriamo -9,  -5,  -3,  -2 ,  - 3 2 ,  - 5 4 ,  - 7 8 , ........ -(½)k-4-1 ,  ..... 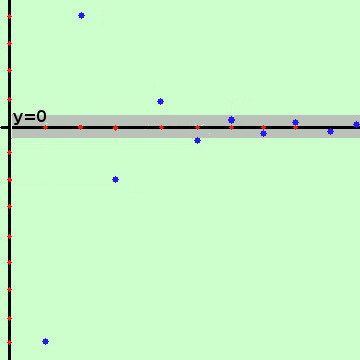Essa ha come limite il valore -1: i suoi termini si avvicinano al valore -1 decrescendo Da un certo momento in poi tutti i termini della successione sono contenuti nella striscia colorata (intorno inferiore di -1 che posso restringere quanto voglio), quindi posso scrivere limk→∞ - (½) k-4   -1 = -1 Successione oscillante a limite finito Esempio: prendiamo la successione gia' considerata -8, +4, -2, +1, -½, +¼.... (-½)n-4, ..... Essa ha come limite il valore 0: i suoi termini si avvicinano al valore 0 sia dall'alto che dal basso (oscillando) Da un certo momento in poi tutti i termini della successione sono contenuti nella striscia colorata (intorno completo di 0 che posso restringere quanto voglio), quindi posso scrivere limk→∞ (-½)k-4 = 0