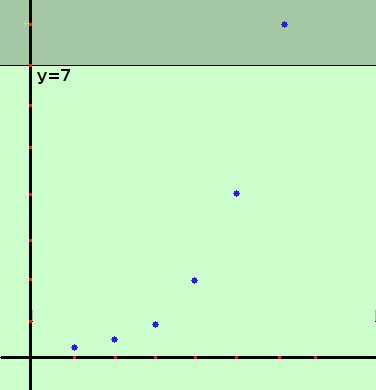
tipi di successioni a limite infinito Distinguiamo i casi Successione crescente a limite infinito Esempio: consideriamo ¼,  ½,   1,   2,   4,   8,  ..... 2n-3, .... 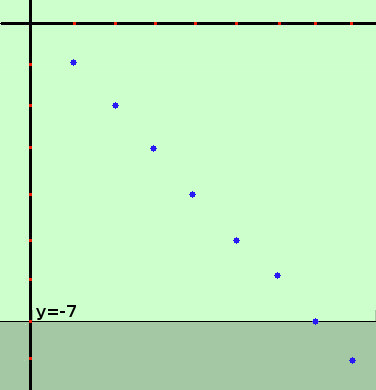Essa tende a +∞: i suoi termini si avvicinano al valore +∞ crescendo Da un certo momento in poi tutti i termini della successione sono contenuti nella striscia colorata (intorno di +∞ che posso spingere verso l'alto quanto voglio: qui ho preso il valore +7 come bordo della striscia), quindi posso scrivere limk→∞ 2k-3 = +∞ Successione decrescente a limite infinito Esempio: consideriamo la successione semplicissima -1, -2, -3, -4, -5, ...... -n, ..... 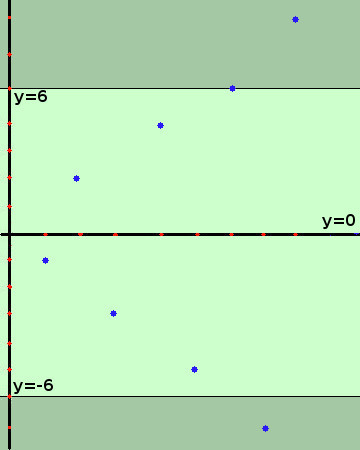Essa tende al valore -∞: i suoi termini si avvicinano al valore -∞ decrescendo Da un certo momento in poi tutti i termini della successione sono contenuti nella striscia colorata (intorno di -∞ che posso spostare in basso quanto voglio: qui ho preso il valore -7 come bordo della striscia), quindi posso scrivere limk→∞ -k = -∞ Successione oscillante tendente ad infinito Esempio: prendiamo la successione -1, +2, -3, +4, -5, +6, -7, +8, ..... n·(-1)n, .... Essa tende al valore ∞ (senza segno): i suoi termini si avvicinano al valore ∞ sia verso l'alto che verso il basso (oscillando) Da un certo momento in poi tutti i termini della successione sono contenuti nella striscia colorata (intorno completo di ∞ che posso spostare verso infinito quanto voglio), quindi posso scrivere limk→∞k·(-1)k = ∞ Approfondimento: perche' l'intorno di infinito (senza segno) e' fatto da due strisce, una verso l'alto ed una verso il basso